
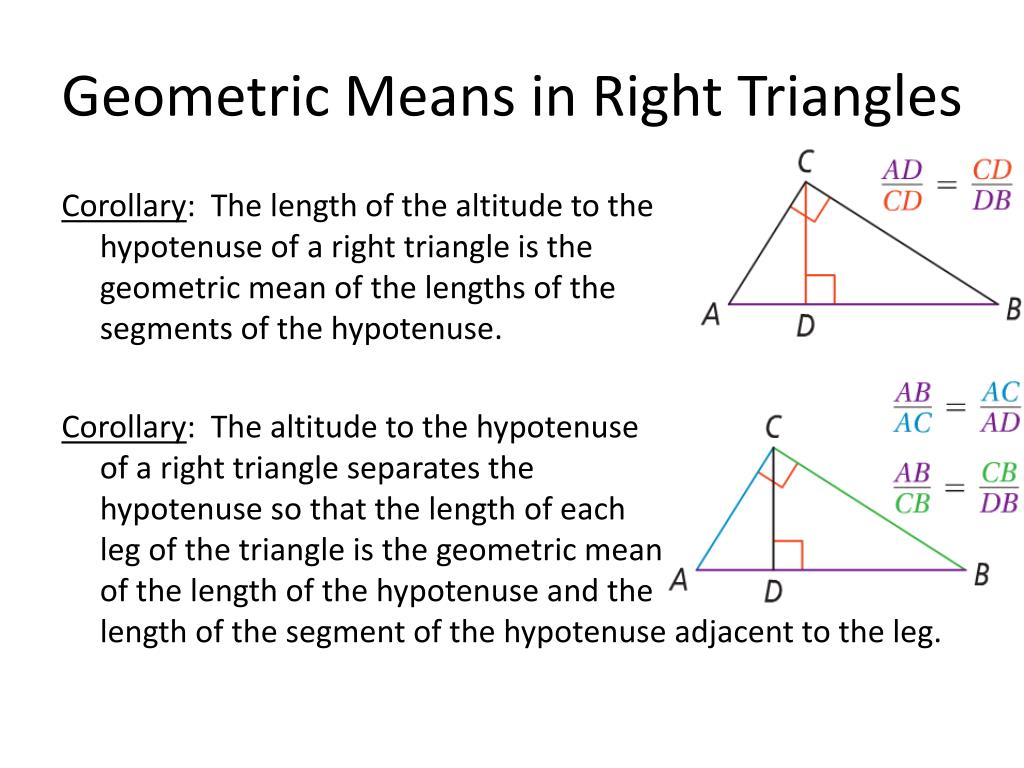

The center of the nine-point circle lies at the midpoint between the orthocenter and the circumcenter, and the distance between the centroid and the circumcenter is half that between the centroid and the orthocenter. The orthocenter, the centroid, the circumcenter and the center of the nine-point circle all lie on a single line, known as the Euler line. Thus for acute and right triangles the feet of the altitudes all fall on the triangle's interior or edge. If one angle is a right angle, the orthocenter coincides with the vertex of the right angle. does not have an angle greater than or equal to a right angle). The orthocenter lies inside the triangle if and only if the triangle is acute (i.e. The three altitudes intersect in a single point, called the orthocenter of the triangle. If we denote the length of the altitude by h c, we then have the relation In a right triangle, the altitude with the hypotenuse c as base divides the hypotenuse into two lengths p and q. It is common to mark the altitude with the letter h (as in height), often subscripted with the name of the side the altitude comes from. Also the altitude having the incongruent side as its base will form the angle bisector of the vertex. In an isosceles triangle (a triangle with two congruent sides), the altitude having the incongruent side as its base will have the midpoint of that side as its foot. The altitudes are also related to the sides of the triangle through the trigonometric functions. Thus the longest altitude is perpendicular to the shortest side of the triangle. It is a special case of orthogonal projection.Īltitudes can be used to compute the area of a triangle: one half of the product of an altitude's length and its base's length equals the triangle's area. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude of that vertex. The length of the altitude, often simply called the altitude, is the distance between the base and the vertex. The intersection between the extended base and the altitude is called the foot of the altitude. This line containing the opposite side is called the extended base of the altitude. forming a right angle with) a line containing the base (the opposite side of the triangle).

In geometry, an altitude of a triangle is a straight line through a vertex and perpendicular to (i.e. The sides a/2 and h are the legs and a the hypotenuse.Three altitudes intersecting at the orthocenterĪn altitude is the perpendicular segment from a vertex to its opposite side. The sides a, a/2 and h form a right triangle. The altitude ( h) of the equilateral triangle (or the height) can be calculated from Pythagorean theorem. Acute triangle: the orthocenter is an inner point.
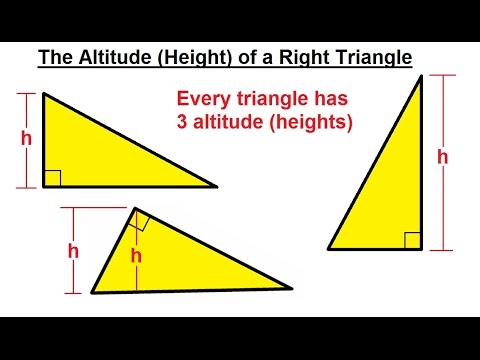
Right triangle: the orthocenter coincides with the right angle’s vertex.Obtuse triangle: the orthocenter is outside the triangle.Acute triangle: all three altitudes lie inside the triangle.Right triangle: The altitude with respect to the hypotenuse is interior, and the other two altitudes coincide with the legs of the triangle.Obtuse triangle: The altitude related to the longest side is inside the triangle (see h c, in the triangle above) the other two heights are outside the triangle (h a, and h b).The altitude can be inside the triangle, outside it, or even coincide with one of its sides, it depends on the type of triangle it is: The three altitudes of a triangle (or its extensions) intersect at a point called orthocenter.


 0 kommentar(er)
0 kommentar(er)
